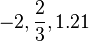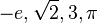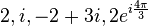matematicaunsaac

Sacar factor común en operaciones con números

Sacar factor común consiste en encontrar el elemento común a un conjunto de sumandos, una operación numérica a veces se simplifica sacando factor común para realizar la operación. Ten presente la propiedad distributiva y observa los ejemplos para ver como se usa el factor común.

Para poder sacar factor común hay que tener presente la propiedad distributiva del producto respecto de la suma que dice

$a\;\cdot\;b\;+\;a\;\cdot\;c\;=\;a\;\cdot\;(b\;+\;c)$

Nota: En el caso numérico el factor común es el máximo común divisor de los sumandos

$\fs25\cdot3\;+\;5\cdot4\;=\;5\cdot(3\;+\;4)\;=\;5\cdot7\;=\;35$	factor común 5
$\fs24\cdot3\;+\;6\cdot3\;-\;8\cdot3\;=\;(4\;+\;6\;-\;8)\cdot3\;=\;2\cdot3=6$	factor común 3
$\frac{2}{3}\cdot\frac{1}{5}\;+\;\fra{8}{15}\;=\;\frac{2}{3}\cdot\frac{1}{5}\;+\;\fra{2}{3}\cdot\frac{4}{5}\;=\;\frac{2}{3}$\frac{1}{5}\;+\;\frac{4}{5}$\;=\;\frac{2}{3}$	factor común $\frac{2}{3}$
$\fs244+64-132+52\;=\;4\cdot(11+16-33+13)\;=\;4\cdot7\;=\;28$

Suma de polinomios.Para sumar polinomios, sumamos entre sí aquellos monomios que tengan la misma parte literal.

Por ejemplo, consideremos los polinomios
P(x)= 3x⁵ + 2x³ - 5x² + 6 y Q(x) = 8x³ + 3x² - x - 4
El polinomio resultante de la suma P(x) + Q(x)= 3x⁵ + 10x³ - 2x² - x + 2
Fíjate, aquellos monomios cuya parte literal aparece en un polinomio los hemos copiado y hemos sumado aquellos monomios que tenían la misma parte literal:
2x³ + 8x³= 10x³-5x² + 3x²= -2x³6 - 4 = 2

Resta de polinomios.Para restar polinomios, restamos entre sí aquellos monomios que tengan la misma parte literal.

Por ejemplo, consideremos los polinomios
P(x)= 3x⁵ + 2x³ - 5x² + 6 y Q(x) = 8x³ + 3x² - x - 4
El polinomio resultante de la resta P(x) - Q(x)= 3x⁵ - 6 x³ - 8x² + x + 10
Fíjate, aquellos monomios cuya parte literal aparece sólo en P(x) se dejan tal cual, a los que aparecen sólo en Q(x) se les cambia el signo y restamos aquellos monomios que tenían la misma parte literal:
2x³ - 8x³= -6x³-5x² - 3x²= -8x³6 - (-4) = 10

Producto de polinomios.Para multiplicar dos polinomios multiplicamos cada monomio del primer polinomio por cada polinomio del segundo. Luego sumamos aquellos monomios con la misma parte literal.

Regla de Ruffini
La regla de Ruffini es un algoritmo que permite obtener fácilmente el cociente y el resto de la división de un polinomio por un binomio de la forma x-a. Veamos el algoritmo con un ejemplo, consideremos P(x)=2x³ + x² - 3x + 5 y Q(x)=x-1. La división se realiza como sigue:

1.Se ordena el polinomio P(x) de mayor a menor grado y se colocan los coeficientes de cada término . Si no apareciese algún término entre el de mayor grado y el de menor se coloca un 0. A la izquierda se pone el número que se resta a x en Q(x), en nuestro caso 1 y se baja el coeficiente del término de mayor grado, este paso se corresponde con la figura 1.

2. Se multiplica el coeficiente que se ha bajado (2) por el que se ha colocado a la izquierda (1). El resultado del producto se coloca debajo del coeficiente del término siguiente y se suman. Figura 2

3. El resultado de la suma se vuelve a multiplicar por el número situado a la izquierda y se repite el proceso. Figuras 3 y 4.

4. El último número (recuadro rojo en Fig. 4) se corresponde con el resto de la división mientras que el resto de números de la fila inferior son los coeficientes del cociente.
Resto = 5 y C(x)=2x² + 3x por tanto 2x³ + x² - 3x + 5 =(x-1) (2x² + 3x) +5

publicacion de marco cesar cuyo sumire

La inspiración, las matemáticas puras y aplicadas y la estética

Véase también: Belleza matemática.

Es muy posible que el arte del cálculo

Sir Isaac Newton (1643-1727), comparte con Leibniz la autoría del desarrollo del cálculo integral y diferencial.

haya sido desarrollado antes incluso que la escritura,^[11] relacionado fundamentalmente con la contabilidad y la administración de bienes, el comercio, en la agrimensura y, posteriormente, en la astronomía.
Actualmente, todas las ciencias aportan problemas que son estudiados por matemáticos, al mismo tiempo que aparecen nuevos problemas dentro de las propias matemáticas. Por ejemplo, el físico Richard Feynman propuso la integral de caminos como fundamento de la mecánica cuántica, combinando el razonamiento matemático y el enfoque de la física, pero todavía no se ha logrado una definición plenamente satisfactoria en términos matemáticos. Similarmente, la teoría de las cuerdas, una teoría científica en desarrollo que trata de unificar las cuatro fuerzas fundamentales de la física, sigue inspirando a las más modernas matemáticas.^[12]
Algunas matemáticas solo son relevantes en el área en la que estaban inspiradas y son aplicadas para otros problemas en ese campo. Sin embargo, a menudo las matemáticas inspiradas en un área concreta resultan útiles en muchos ámbitos, y se incluyen dentro de los conceptos matemáticos generales aceptados. El notable hecho de que incluso la matemática más pura habitualmente tiene aplicaciones prácticas es lo que Eugene Wigner ha definido como la irrazonable eficacia de las matemáticas en las Ciencias Naturales.^[13]
Como en la mayoría de las áreas de estudio, la explosión de los conocimientos en la era científica ha llevado a la especialización de las matemáticas. Hay una importante distinción entre las matemáticas puras y las matemáticas aplicadas. La mayoría de los matemáticos que se dedican a la investigación se centran únicamente en una de estas áreas y, a veces, la elección se realiza cuando comienzan su licenciatura. Varias áreas de las matemáticas aplicadas se han fusionado con otras áreas tradicionalmente fuera de las matemáticas y se han convertido en disciplinas independientes, como pueden ser la estadística, la investigación de operaciones o la informática.
Aquellos que sienten predilección por las matemáticas, consideran que prevalece un aspecto estético que define a la mayoría de las matemáticas. Muchos matemáticos hablan de la elegancia de la matemática, su intrínseca estética y su belleza interna. En general, uno de sus aspectos más valorados es la simplicidad. Hay belleza en una simple y contundente demostración, como la demostración de Euclides de la existencia de infinitos números primos, y en un elegante análisis numérico que acelera el cálculo, así como en la transformada rápida de Fourier. G. H. Hardy en A Mathematician's Apology (Apología de un matemático) expresó la convicción de que estas consideraciones estéticas son, en sí mismas, suficientes para justificar el estudio de las matemáticas puras.^[14] Los matemáticos con frecuencia se esfuerzan por encontrar demostraciones de los teoremas que son especialmente elegantes, el excéntrico matemático Paul Erdős se refiere a este hecho como la búsqueda de pruebas de "El Libro" en el que Dios ha escrito sus demostraciones favoritas.^[15] ^[16] La popularidad de la matemática recreativa es otra señal que nos indica el placer que produce resolver las preguntas matemáticas.

Notación, lenguaje y rigor

Artículo principal: Notación matemática.

Leonhard Euler. Probablemente el más prolífico matemático de todos los tiempos.

La mayor parte de la notación matemática que se utiliza hoy en día no se inventó hasta el siglo XVIII.^[17] Antes de eso, las matemáticas eran escritas con palabras, un minucioso proceso que limita el avance matemático. En el siglo XVIII, Euler, fue responsable de muchas de las notaciones empleadas en la actualidad. La notación moderna hace que las matemáticas sean mucho más fácil para los profesionales, pero para los principiantes resulta complicada. La notación reduce las matemáticas al máximo, hace que algunos símbolos contengan una gran cantidad de información. Al igual que la notación musical, la notación matemática moderna tiene una sintaxis estricta y codifica la información que sería difícil de escribir de otra manera.

El símbolo de infinito en diferentes tipografías.

El lenguaje matemático también puede ser difícil para los principiantes. Palabras tales como o y sólo tiene significados más precisos que en lenguaje cotidiano. Además, palabras como abierto y cuerpo tienen significados matemáticos muy concretos. La jerga matemática, o lenguaje matemático, incluye términos técnicos como homeomorfismo o integrabilidad. La razón que explica la necesidad de utilizar la notación y la jerga es que el lenguaje matemático requiere más precisión que el lenguaje cotidiano. Los matemáticos se refieren a esta precisión en el lenguaje y en la lógica como el "rigor".
El rigor es una condición indispensable que debe tener una demostración matemática. Los matemáticos quieren que sus teoremas a partir de los axiomas sigan un razonamiento sistemático. Esto sirve para evitar teoremas erróneos, basados en intuiciones falibles, que se han dado varias veces en la historia de esta ciencia.^[18] El nivel de rigor previsto en las matemáticas ha variado con el tiempo: los griegos buscaban argumentos detallados, pero en tiempos de Isaac Newton los métodos empleados eran menos rigurosos. Los problemas inherentes de las definiciones que Newton utilizaba dieron lugar a un resurgimiento de un análisis cuidadoso y a las demostraciones oficiales del siglo XIX. Ahora, los matemáticos continúan apoyándose entre ellos mediante demostraciones asistidas por ordenador.^[19]
Un axioma se interpreta tradicionalmente como una "verdad evidente", pero esta concepción es problemática. En el ámbito formal, un axioma no es más que una cadena de símbolos, que tiene un significado intrínseco sólo en el contexto de todas las fórmulas derivadas de un sistema axiomático.

[editar] La matemática como ciencia

Carl Friedrich Gauss, apodado el "príncipe de los matemáticos", se refería a la matemática como "la reina de las ciencias".

Carl Friedrich Gauss se refería a la matemática como "la reina de las ciencias".^[20] Tanto en el latín original Scientiarum Regina, así como en alemán Königin der Wissenschaften, la palabra ciencia debe ser interpretada como (campo de) conocimiento. Si se considera que la ciencia es el estudio del mundo físico, entonces las matemáticas, o por lo menos matemáticas puras, no son una ciencia.
Muchos filósofos creen que las matemáticas no son experimentalmente falseables, y, por tanto, no es una ciencia según la definición de Karl Popper.^[21] No obstante, en la década de 1930 una importante labor en la lógica matemática demuestra que las matemáticas no puede reducirse a la lógica, y Karl Popper llegó a la conclusión de que "la mayoría de las teorías matemáticas son, como las de física y biología, hipotético-deductivas. Por lo tanto, las matemáticas puras se han vuelto más cercanas a las ciencias naturales cuyas hipótesis son conjeturas, así ha sido hasta ahora".^[22] Otros pensadores, en particular Imre Lakatos, han solicitado una versión de Falsacionismo para las propias matemáticas.
Una visión alternativa es que determinados campos científicos (como la física teórica) son matemáticas con axiomas que pretenden corresponder a la realidad. De hecho, el físico teórico, J. M. Ziman, propone que la ciencia es conocimiento público y, por tanto, incluye a las matemáticas.^[23] En cualquier caso, las matemáticas tienen mucho en común con muchos campos de las ciencias físicas, especialmente la exploración de las consecuencias lógicas de las hipótesis. La intuición y la experimentación también desempeñan un papel importante en la formulación de conjeturas en las matemáticas y las otras ciencias. Las matemáticas experimentales siguen ganando representación dentro de las matemáticas. El cálculo y simulación están jugando un papel cada vez mayor tanto en las ciencias como en las matemáticas, atenuando la objeción de que las matemáticas se sirven del método científico. En 2002 Stephen Wolfram sostiene, en su libro Un nuevo tipo de ciencia, que la matemática computacional merece ser explorada empíricamente como un campo científico.
Las opiniones de los matemáticos sobre este asunto son muy variadas. Muchos matemáticos consideran que llamar a su campo ciencia es minimizar la importancia de su perfil estético, además supone negar su historia dentro de las siete artes liberales. Otros consideran que hacer caso omiso de su conexión con las ciencias supone ignorar la evidente conexión entre las matemáticas y sus aplicaciones en la ciencia y la ingeniería, que ha impulsado considerablemente el desarrollo de las matemáticas. Otro asunto de debate, que guarda cierta relación con el anterior, es si la matemática fue creada (como el arte) o descubierta (como la ciencia). Este es uno de los muchos temas de incumbencia de la filosofía de las matemáticas.
Los premios matemáticos se mantienen generalmente separados de sus equivalentes en la ciencia. El más prestigioso premio dentro de las matemáticas es la Medalla Fields,^[24] ^[25] fue instaurado en 1936 y se concede cada 4 años. A menudo se le considera el equivalente del Premio Nobel para la ciencia. Otros premios son el Premio Wolf en matemática, creado en 1978, que reconoce el logro en vida de los matemáticos, y el Premio Abel, otro gran premio internacional, que se introdujo en 2003. Estos dos últimos se conceden por un excelente trabajo, que puede ser una investigación innovadora o la solución de un problema pendiente en un campo determinado. Una famosa lista de esos 23 problemas sin resolver, denominada los "Problemas de Hilbert", fue recopilada en 1900 por el matemático alemán David Hilbert. Esta lista ha alcanzado gran popularidad entre los matemáticos y, al menos, nueve de los problemas ya han sido resueltos. Una nueva lista de siete problemas fundamentales, titulada "Problemas del milenio", se publicó en 2000. La solución de cada uno de los problemas será recompensada con 1 millón de dólares. Curiosamente, tan solo uno (la Hipótesis de Riemann) aparece en ambas listas.

[editar] Ramas de estudio de las matemáticas

Artículo principal: Áreas de las matemáticas.

Véase también: Categoría:Áreas de las matemáticas.

La Sociedad Americana de Matemáticas distingue unas 5.000 ramas distintas de matemáticas.^[26] Dichas ramas están muy interrelacionadas. En una subdivisión amplia de las matemáticas se distinguen cuatro objetos de estudio básicos: la cantidad, la estructura, el espacio y el cambio^{[cita requerida]} que se corresponden a la aritmética, álgebra, geometría y cálculo. Ademas, hay ramas de las matemáticas conectadas a otros campos como la lógica y teoría de conjuntos, y las matemáticas aplicadas.

Los diferentes tipos de cantidades (números) han jugado un papel obvio e importante en todos los aspectos cuantitativos y cualitativos del desarrollo de la cultura, la ciencia y la tecnología.
El estudio de la estructura comienza al considerar las diferentes propiedades de los números, inicialmente los números naturales y los números enteros. Las reglas que dirigen las operaciones aritméticas se estudian en el álgebra elemental, y las propiedades más profundas de los números enteros se estudian en la teoría de números. Después, la organización de conocimientos elementales produjo los sistemas axiomáticos (teorías), permitiendo el descubrimiento de conceptos estructurales que en la actualidad dominan esta ciencia (e.g. estructuras categóricas). La investigación de métodos para resolver ecuaciones lleva al campo del álgebra abstracta. El importante concepto de vector, generalizado a espacio vectorial, es estudiado en el álgebra lineal y pertenece a las dos ramas de la estructura y el espacio.
El estudio del espacio origina la geometría, primero la geometría euclídea y luego la trigonometría. En su faceta avanzada el surgimiento de la topología da la necesaria y correcta manera de pensar acerca de las nociones de cercanía y continuidad de nuestras concepciones espaciales.
La comprensión y descripción del cambio en variables mensurables es el tema central de las ciencias naturales y del cálculo. Para resolver problemas que se dirigen en forma natural a relaciones entre una cantidad y su tasa de cambio, se estudian las ecuaciones diferenciales y de sus soluciones. Los números usados para representar las cantidades continuas son los números reales. Para estudiar los procesos de cambio se utiliza el concepto de función matemática. Los conceptos de derivada e integral, introducidos por Newton y Leibniz, representan un papel clave en este estudio, y son objetos del Cálculo diferencial e integral y, en cuanto al rigor, se ocupa el Análisis matemático. Es conveniente para muchos fines introducir función, derivación, integración en el conjunto C de los números complejos, así surgen el cálculo de variable compleja y el análisis complejo. El análisis funcional consiste en estudiar los espacios vectoriales de dimensión infinita, problemas cuya incógnita es una función.

[editar] Matemáticas puras

[editar] Cantidad

El estudio de la cantidad comienza con los números, primero con los más familiares: números naturales y enteros, y las operaciones aritméticas entre ellos, que caracteriza la aritmética. Las propiedades más profundas acerca de los números se estudian en la teoría de números, campo matematico que nos ha dado resultados populares como el último teorema de Fermat. La conjetura de los primos gemelos y la conjetura de Goldbach son algunos problemas sin solución de la teoría de números.
Como el sistema de números se desarrolla, los enteros son reconocidos como un subconjunto de los números racionales (fracciones). Estos, a su vez están contenidos en los números reales, que son usados para representar cantidades continuas. Los números reales son generalizables a los números complejos. Estos son los primeros hacia una jerarquía de números que va a incluir a los cuaterniones y octoniones. Tambien destacamos los números transfinitos, que formalizan en concepto de infinito. Otra área de estudio es el tamaño, lo que conduce a los números cardinales y a otra concepción del infinito: los números alef, que permiten comparar el tamaño de conjuntos infinitamente grandes.

$1, 2, 3,\ldots\!$	$\ldots,-2, -1, 0, 1, 2\,\ldots\!$	$-2, \frac{2}{3}, 1.21\,\!$	$-e, \sqrt{2}, 3, \pi\,\!$	$2, i, -2+3i, 2e^{i\frac{4\pi}{3}}\,\!$
Números naturales	Enteros	Números racionales	Números reales	Números complejos

[editar] Estructura

$\begin{matrix} (1,2,3) & (1,3,2) \\ (2,1,3) & (2,3,1) \\ (3,1,2) & (3,2,1) \end{matrix}$
Combinatoría	Teoría de números	Teoría de grupos	Teoría de grafos	Teoría del orden	Álgebra